Member-only story
The NAND gate. One gate to rule them all.
Chronicles of my descent into madness.

Level 1: The human world.
A NAND gate (NOT-AND) is a logic gate which produces an output which is false only if all its inputs are true.
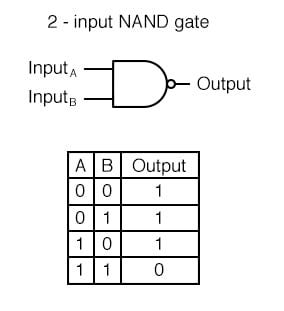
It doesn’t sound too useful from a practical sense. After all, how often are you reasoning about something with two inputs, and you want to figure out what happens exactly when they are both not true at the same time?
Let’s say, for example, that you want to paint a chair red. For that, you need two things: a chair, and a bucket of red paint. Let’s call them “C” and “R”. Let’s say that you have an algorithm CAN_PAINT which takes those inputs and returns true if you can paint the chair. Such an algorithm would use the AND operation.
Now, suppose an algorithm NAND_ALGORITHM exists, which takes C and R as inputs. Can you imagine a practical use-case for such an algorithm? It would returns true only when:
- There is no chair and no red paint.
- There is a chair but no red paint.
- There is red paint but no chair.
For the life of me, I can’t think of anything. I conclude that NAND is rarely a helpful operation on its own, at the human level.
Level 2: The computer world.
So, what’s the big deal? The NAND gate is significant because we can implement any Boolean function using a combination of NAND gates. This property is called “functional completeness”. It turns out this is important for manufacturing computers, at least in a theoretical sense.
But why isn’t the AND gate “functionally complete” too? It’s just the opposite of NAND, right? So I’m sure you can reverse some things here and there and make it work?
The answer is not so easy because it took until 1913 for us to known. All thanks to Henry M. Sheffer, who published this paper in the “Transactions of the American Mathematical Society”. In fact, the NAND gate is also called “Sheffer stroke”.
